Un solide (S) est animé d'un mouvement de translation dans (R) si on a :

1 - Mouvement de translation |
2 - Mouvement de translation rectiligne |
a) Définition |
a) Mouvement de translation rectiligne uniforme |
b) Champs des vecteurs vitesse |
b) Mouvement de translation rectiligne uniformément varié |
c) Champs des vecteurs accélération |
Un solide (S) est animé d'un mouvement de translation dans (R) si on a :
|
 |
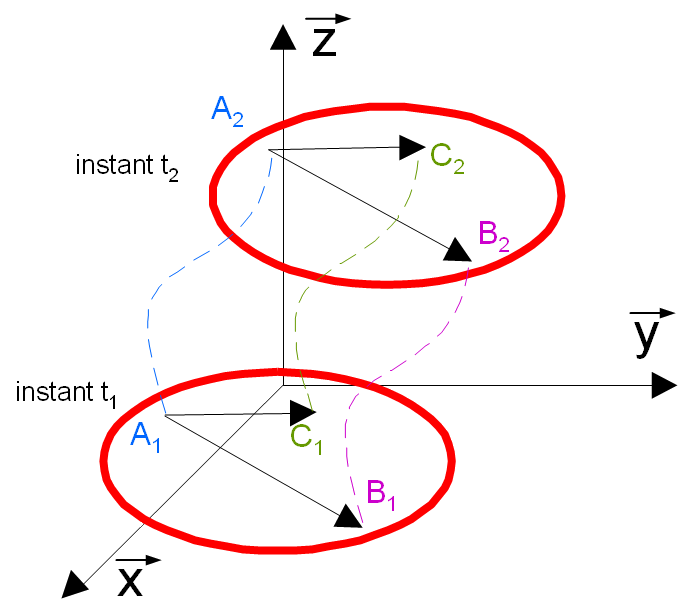
Dans le mouvement de translation d'un solide (S) par rapport à un repère de référence (R), tous les points du solide (S) ont au même instant (t) ont des vecteurs vitesse par rapport à (R) équipollent entre eux. On dit que le champ des vecteurs vitesse est UNIFORME. |
 |
Dans le mouvement de translation d'un solide (S) par rapport à un repère de référence (R), tous les points du solide (S) ont au même instant (t) ont des vecteurs accélération par rapport à (R) équipollent entre eux.
On dit que le champ des vecteurs accélération est UNIFORME.
Pour la suite du cours, on se limitera à l'étude des mouvements de translation rectiligne.
Un mouvement de translation est dit rectiligne si la trajectoire de tous les points du solide (S) en mouvement sont des droites parallèles entre elles. Il en résulte que :
Le champ des vecteurs vitesse et celui des vecteurs accélération ont une direction constante au cours du temps, celle des trajectoires.
Les vecteurs accélération sont des accélérations tangentielles (le rayon de courbure étant infini, l'accélération normale est nulle
|
 |
On choisi généralement un des axes du repère de référence de même direction que les trajectoires des points du solide (S).
Un mouvement de translation rectiligne est UNIFORME si la vitesse est constante au cours du temps. Il en résulte que l'accélération est donc nulle. |
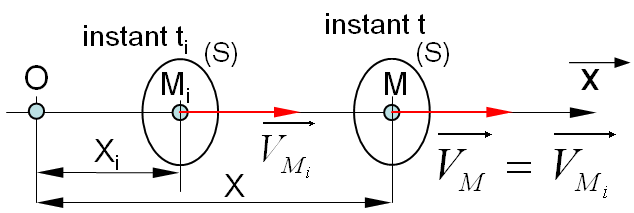 |
Équations paramétriques :
Accélération : |
Avec :
|
|
|
Vitesse : (m/s) |
|
|
|
Position (abscisse) : (m) |
|
|
Représentations graphiques :
On s'aperçoit que la vitesse étant constante, courbe fuschia, la position, courbe marron, croît de manière linéaire.

Un mouvement de translation rectiligne est UNIFORMÉMENT VARIÉ si l'accélération est constante et non nulle au cours du temps. |
 |
Équations paramétriques :
Accélération : |
Avec :
|
|
|
Vitesse : (m/s) |
|
|
|
Position (abscisse) : (m) |
|
Représentations graphiques :
on s'aperçoit que la vitesse, courbe fuschia, croît de manière linéaire, et donc la position, courbe marron, augmente de manière parabolique.
